Force, Duration and Speed

Relationship between force, mass, and acceleration. The acceleration of an object (in a given direction) is caused by (a) the net force acting on the object in that direction and (b) the mass of the object. This is Newton's second law. If the net force acting on an object in a direction is zero, then the object's acceleration in that direction would also be zero. You can easily check for yourself by plugging zero in for the net force into Newton's Second Law equation (below) to find the acceleration:

Check your understanding...

Q1: An object is moving horizontally at a speed of 10 m/s. The only forces acting on the object are gravity and the force of the ground pushing upward. The object's speed will:

a) Increase

b) Decrease

c) Stay the same

d) More information is needed to answer.

Right! The object is moving in the horizontal direction. The only forces acting on the object are in the vertical direction. So, there are no forces acting on the body in the horizontal direction. Because of this, the body's acceleration in the horizontal direction will be zero. This means that the object's velocity (or speed in this direction) will not change.

Actually, the object is moving in the horizontal direction. The only forces acting on the object are in the vertical direction. So, there are no forces acting on the body in the horizontal direction. Because of this, the body's acceleration in the horizontal direction will be zero. This means that the object's velocity (or speed in this direction) will not change.

If the net force acting on the object in a given direction is not equal to zero, the object's speed will change, or it will accelerate, in that direction for as long as the force acts on the object.

Example 1. Force A (10 Newtons) acts on an object-that is initially at rest-in the horizontal direction. Because the object is on an ice surface, there is no friction acting on the object. So, the only force acting on the object in the horizontal direction is Force A. The force is constant (meaning it does not change; it is always 10 N) and keeps acting on the object all the way across the ice (to after Point D, shown below). So, the speed of the object will keep increasing all the way across the ice. It will be slowest at Point A, faster at Point B, still faster at Point C and fastest at Point D.

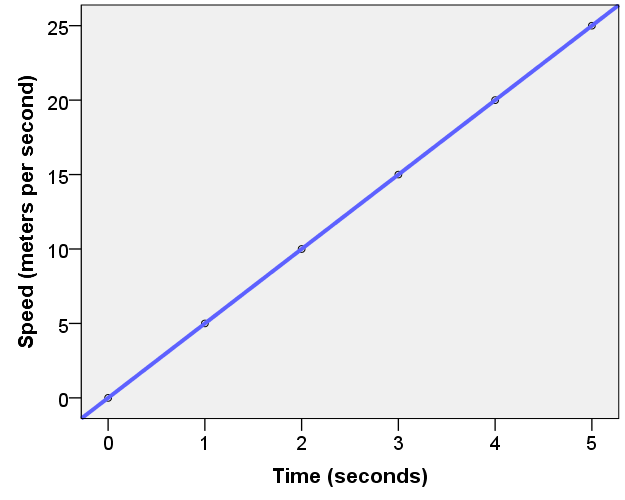
Because the object was pushed by a constant force (10 N) all the way across the ice, the acceleration of the object will also be constant (or will not change). A constant acceleration means that every second, the object's speed will increase by the same amount. If the object had a mass of 2 kg, then its acceleration would be 5 m/s² (because, applying Newton's Second Law, 10 N divided by 2 kg is 5 m/s²). This means that every second the force acts on the object, its speed increases by 5 m/s. This constant acceleration of 5 m/s² is shown in the graph below.

Reminder: If the net force acting on an object in a given direction is not equal to zero, the object will accelerate in that direction for as long as the force acts on the object.

But, the moment the net force in that direction is zero, the object will no longer accelerate in that direction. So, in Example 1 (shown above), if Force A stops acting on the object at Point C, the object would also stop accelerating at Point C.

Q2: True or false: After you throw a ball (and you are no longer touching it), there will still be some "leftover" force from your throw acting on the ball.

a) True

b) False

c) I have no idea.

Right! While you are touching the ball, your hand is exerting a force on the ball (pushing the ball). But once you let the ball go, you are no longer pushing on the ball. So, there is no force from your hand acting on the ball after you throw it.

Actually, while you are touching the ball, your hand is exerting a force on the ball (pushing the ball). But once you let the ball go, you are no longer pushing on the ball. So, there is no force from your hand acting on the ball after you throw it.

Q3: In the scenario of Example 1, shown above, in Case A, the force acts on the object from the starting point to point A. In Case B, the same force acts on the object from the starting point to point B. In which case would the speed of the object be greater at point D?

a) Case A

b) Case B

c) The speeds would be the same in both Cases.

d) I don't know.

You're right! The object would accelerate (only) while the force is acting on the object. So, the force acts on the object for a longer period of time in Case B than Case A. As a result, the object's speed at point D would be greater in Case B.

Well actually, the object would accelerate (only) while the force is acting on the object. So, the force acts on the object for a longer period of time in Case B than Case A. As a result, the object's speed at point D would be greater in Case B.

Q4: In the scenario of Example 1 above, a constant force pushes on the object to the right from its starting position to point B. After point B, there is no horizontal force acting on the body. Which of the lines on the graph to the left best shows the speed of the object from its starting point to point D?

a) L1

b) L2

c) L3

d) L4

That's right! The object would accelerate (or increase in speed) while the force is acting on the object. So, the object's speed would increase from its starting point to point B. At point B, there are no forces acting on the object in the horizontal direction. So, the speed would remain constant after point B (constant speed is shown as a horizontal line on the graph).

Well actually, the object would accelerate (or increase in speed) while the force is acting on the object. So, the object's speed would increase from its starting point to point B. At point B, there are no forces acting on the object in the horizontal direction. So, the speed would remain constant after point B (constant speed is shown as a horizontal line on the graph).