What is Friction? Friction is a force between a surface and an object moving on that surface that resists motion. In other words, the force of friction acts in the direction that is opposite the direction the object is moving on a surface. This idea is shown below, where a person pushes on a box to the right. The force of friction acts on the box in the opposite direction (to the left):
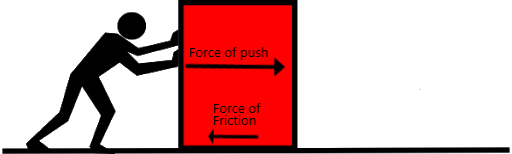
Why do we care about friction? Friction is another very important force that allows you to walk, ride your bike, or drive to where you want to go. Without friction, we'd slide off of our chairs and slip trying to walk! It would be as if every surface were as slippery as the most slippery ice!
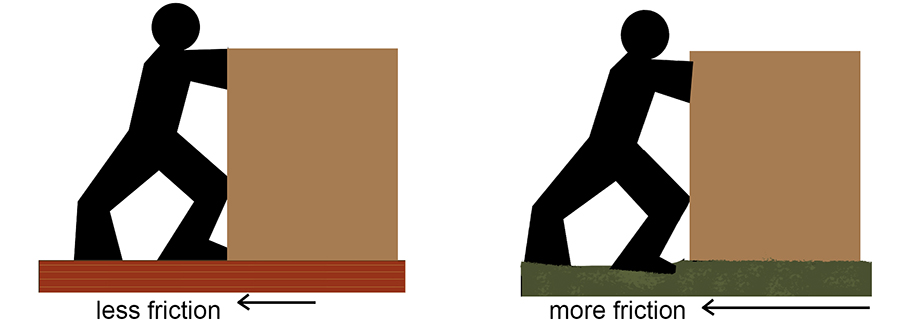
Example 1. You have probably noticed that it's much easier to push a box on a wooden floor than on a carpeted floor. This is because there is more friction that opposes the motion of the box on the carpeted floor than on the smoother wooden floor.
Example 2. For example, when you walk barefoot, you may feel the friction between the bottom of your foot and the ground surface. When you first take a step and push forward on the ground (See #1 in the picture below), this friction force acts on your foot in the opposite direction you are walking in. The amount of the force of friction acting on your foot is also the same as the force your foot applies to the ground. This balance of forces keeps your foot from sliding forward on the ground. But if you stepped on a banana, the backward friction force would be much less. As a result, your foot would slide forward, in the direction of the net force acting on your foot (and you may fall!).
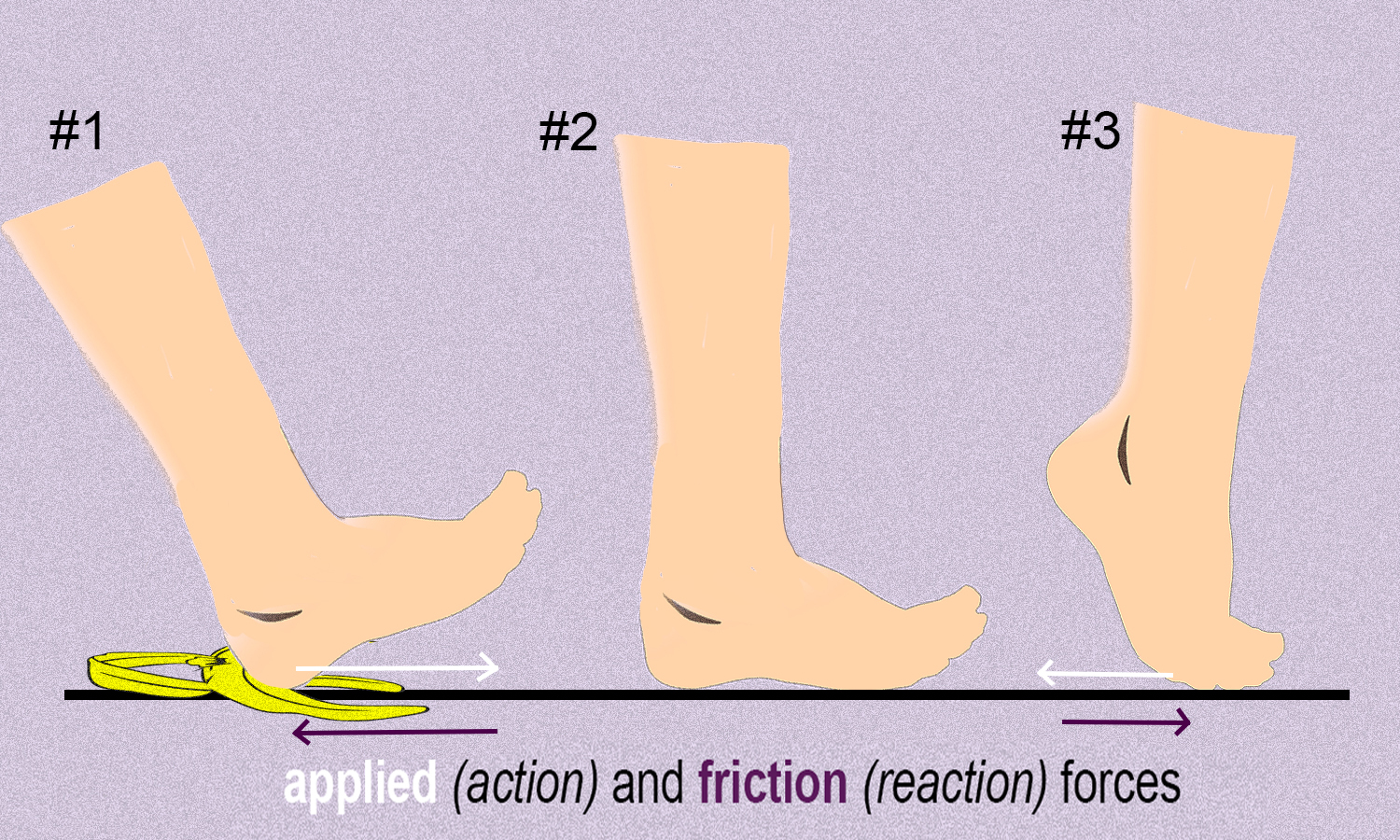
So, this shows how the friction between the ground and the bottom of your foot is necessary to keep your foot from sliding forward when you first take a step. This happens because friction pushes against the bottom of your foot in the opposite direction that you are pushing against the ground. The amount of the force of friction acting on your foot is also the same as the force your foot applies to the ground.
As shown in #3, friction also allows you to push off backward on the ground and allow you to move forward. Friction acts in the opposite direction of your push on the ground, or forward this time. If there were less or no friction (for example, if you stepped on another banana), your foot would slide backwards and you may fall (again!).
Example 3. For a round object to roll down an incline (such as a hill), there must be at least some friction between the object and surface of the incline. If there is no friction, the object will not roll. Instead, it will slide down the incline.
Effect of friction on sliding vs. rolling objects. The amount of friction between a round object (for example, a ball) and surface determines whether the object will slide or roll on the surface (for example, a ramp).
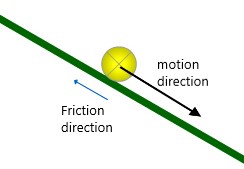
If there is no or little friction, the object will slide down the surface. This is represented in the picture below. For sliding objects, greater friction produces more resistance to the object's motion.
If there is enough friction acting on the round object (as shown below), it will start to roll down the surface. This is what we see happen most of the time.
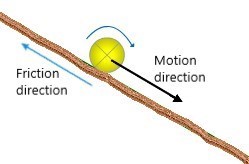
Once there is enough friction to keep the rolling object rolling (and not slipping or sliding at all on the surface), increasing the friction does not affect the rolling object's motion. In other words, once friction is greater than a certain amount, adding more friction does not affect the ball's motion.
Friction and speed of ball on ramp. As discussed more in Kinetic and Potential Energy (advanced section), there are several types of kinetic energy (KE). One type is translational KE, which is the energy due to the movement of the object across a distance (for example, a ball sliding down a ramp). The faster an object moves, the greater its translational KE is.
Another type of KE is rotational KE. This is the energy due to an object's rotation around an axis. The faster the object rotates, the greater its rotational KE is. Both types of motion are shown in the animation below:
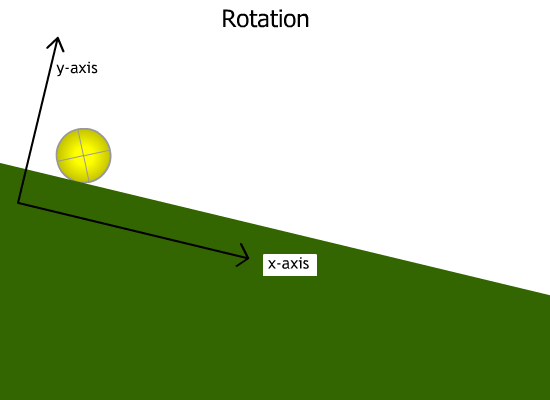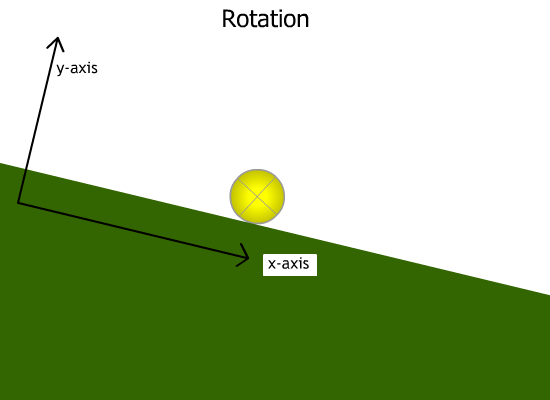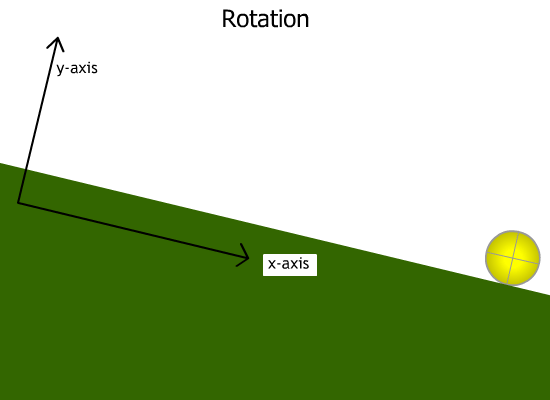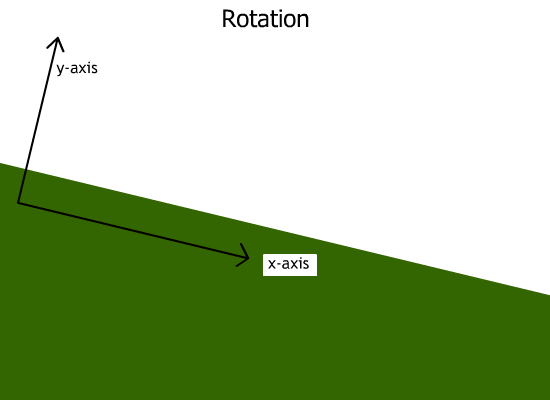
The animation above shows a ball rolling down a ramp. The ball has two types of motion: (a) translational motion (moving along the x-axis, and (b) rotational motion (rotating along its own axis).
Advanced!!: The acceleration of a solid sphere rolling down an incline without slipping. (This section includes concepts related to rotational motion that are probably not familiar to students.)
The animation above shows a ball rolling down a ramp. The ball has two types of motion: (a) translational motion (moving along the x-axis, and (b) rotational motion (rotating along its own axis).
Applying Newton's Second Law in x-direction (down the ramp): m • ax = m • g • sinΘ - fs (#1)
Plan for solving for ax: We want to reduce the number of unknowns in this equation by replacing fs with other terms in the equation (like acceleration and mass). To do that, we will use something called the torque (pronounced "tork"). Torque is a twisting force that causes objects to spin/rotate/roll. We will use this relationship for the torque on the ball.
Sum of Torque on object = I • α = fs • r (#2) (because the only torque acting on the ball is due to friction)
This is analogous to Newton's second law: The Sum of Forces on object = m • a; The Sum of Torque on an object = I • α, where:
For a solid sphere:
I = 2/5 m • r2 (#3) (r: radius of sphere)
α = ax / r (#4)
Solving for fs (in #2):
fs = I • α/r
Substituting for I (#3) & α (#4):
fs = (2/5 m • r2)(ax/r)/r
fs= 2/5 m • ax (#5)
Substituting fs from (#4) into our original equation (#1):
m • ax = m • g • sinΘ - 2/5 m • ax
The m's (mass) cancel each other, and we have:
ax = g • sinΘ - 2/5 ax
Adding 2/5 ax to both sides of the equation:
7/5 ax = g • sinΘ
And Finally!!...
ax = 5/7 g • sinΘ ==> This is the acceleration of a solid sphere rolling without slipping down a ramp.
If there were no friction on this ramp, then from (#1):
ax ax = g • sinΘ or ax = 7/7 g • sinΘ
So, we see that the acceleration of the ball down the ramp, ax is less when the ball is rolling due to friction on the ramp surface compared to when it slides down the ramp with no friction.
***Note for Teachers: You can access more information about this website and find other resources for science inquiry on the ISP Tutor website.
©2022 Klahr Lab. All Rights Reserved
The TED project was funded in part by the Institute of Education Science (IES), Grant R305H060034, and in part by the National Science Foundation, Grant SBE035442. The ISP Tutor project was funded by IES, Grant R305A170176.
The research reported here was supported by the Institute of Education Sciences, U.S. Department of Education, through Grant R305A170176 to Carnegie Mellon University (Klahr Lab). The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Department of Education.