Surface Area

What is Surface Area? The surface area of an object is defined as the total area of the surface of the 3-dimensional object. The surface is the outermost region of an object.

In this unit, we will calculate surface area of various shapes with smooth surfaces.

Surface Area of Cubes

Example of calculating surface area of sphere: As shown below, the diameter of a cube is 3 cm.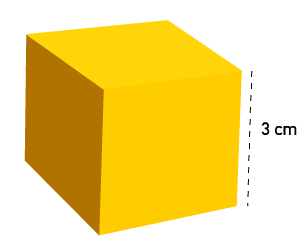

So, each of the faces (sides) of the cube has an area of 3 x 3, or 9 cm². A cube has

So, the total surface area of the cube would be 6 x 9 cm², or 54 cm². Cubewith3cmside

In general, the surface area of a cube of diameter, d, is equal to: d² (area per side) × 6 (sides) = 6d²

Surface area of Cube = 6d²

Surface Area of Spheres

In general, the surface area of a sphere of radius, r, is equal to 4 πr².

In this equation, π is "pi", which is 3.1415..., or about 3.

The radius of a circle is equal to half of its diameter: r = d/2.

We can substitute "d/2" for "r" in the formula above:

4π(d/2)² = 4πd²/4 = πd²

So...

Surface area of Sphere = πd²

Example of calculating surface area of sphere: A sphere has a diameter of 4 cm. We can calculate the surface area of the sphere, which is the area of the outer part of the sphere (that we can touch/feel) by using this formula:

Surface area (of a sphere) = πd²
Surface area (sphere) = 3.14 × 4²= 3.14 × 16 = 50.27 cm²

Q1: Which would have a bigger surface area: a sphere with a diameter of 10 cm or a cube with a diameter of 10 cm?

a) the sphere

b) the cube

c) they would have the same surface areas

d) I have no idea.

Right! In general, if a cube and sphere have the same diameter, the cube has greater surface area. This is because the surface area of a sphere is pi (about 3) times the diameter squared. And the surface area of a cube is 6 times the cube's diameter squared. So, for any cube and sphere of the same diameter, the surface area of the cube will be almost *twice* that of the sphere!

Actually, in general, if a cube and sphere have the same diameter, the cube has greater surface area. This is because the surface area of a sphere is pi (about 3) times the diameter squared. And the surface area of a cube is 6 times the cube's diameter squared. So, for any cube and sphere of the same diameter, the surface area of the cube will be almost *twice* that of the sphere!

Q2: Sphere A has a diameter of D. Sphere B has a diameter of 2D (Sphere B's diameter is twice Sphere A's diameter). Which is true of the surface areas of the spheres?

a) Sphere A and B have the same surface areas.

b) Sphere B has twice the surface area of Sphere A.

c) Sphere B has three times the surface area of Sphere A.

d) Sphere B has four times the surface area of Sphere A.

That's right! Sphere B's surface area would be four times that of Sphere A. This is because the surface area of a sphere is given by: 𝜋d². So, for Sphere A, the surface area is 𝜋D² For Sphere B, the surface area is 𝜋(2D)² = 4𝜋D²

Actually, Sphere B's surface area would be four times that of Sphere A. This is because the surface area of a sphere is given by: 𝜋d². So, for Sphere A, the surface area is 𝜋D² For Sphere B, the surface area is 𝜋(2D)² = 4𝜋D²

Surface area (for non-smooth surfaces)

When we calculated the surface area of the objects above, we assumed that the surfaces were completely smooth. But if the surfaces were bumpy instead of smooth, their surface areas would be larger. For example, a golf ball, which has dimples on its surface, has more surface area than a smooth ball of the same (average) radius.

Q3: Two spherical balls (A & B) are made of the same bumpy material. Ball A has a diameter twice that of Ball B. Which is true of the number of bumps on each ball?

a) There are the same number of bumps on A and B.

b) Ball A has twice the number of bumps as Ball B.

c) Ball A has three times the number of bumps as Ball B.

d) Ball A has four times the number of bumps as Ball B.

You're right! Because Ball A's diameter is twice that of Ball B, it will have FOUR times the surface area as Ball B. So, it will also have about 4 times the number of bumps on its surface as Ball B.

Actually, because Ball A's diameter is twice that of Ball B, it will have FOUR times the surface area as Ball B. So, it will also have about 4 times the number of bumps on its surface as Ball B.

Surface area to volume ratio for sphere

In general, as the diameter of a sphere increases, the ratio of its surface area to its volume decreases. That is, as the diameter of a sphere increases, the sphere will have LESS surface area per given volume of space. Or, as the diameter of a sphere increases, the sphere will have MORE volume per surface area.

Surface area of sphere: πd²
Volume of sphere: πd³/6

So, Surface Area/Volume of sphere: 6/d

OR...

Volume/Surface Area of sphere: d/6

Surface Area

Table of Contents: Surface Area unit